Absolute Value Of Correlation Coefficient

Correlation – Correlation coefficient, r

iii mins read

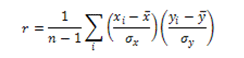
The correlation coefficient is a measure of the strength and direction of a linear relationship between ii variables. It may be calculated using the following formula:

Where

n is the sample size
10_i is the measurement for the ith ascertainment of variable x
x_bar is the hateful of all the observations of variable x
σ_xis the standard deviation of the observations of variable x
y_i is the measurement for the ith observation of variable y
y_bar is the mean of all the observations of variable y
σ_yis the standard deviation of the observations of variable y

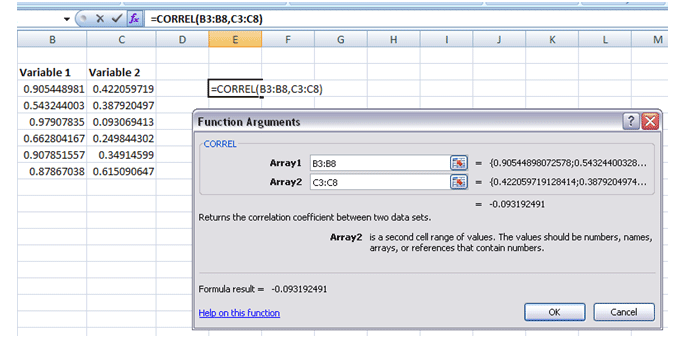
Alternately, it may exist calculated in EXCEL using the office CORREL():

If you accept more than ii sets of information fourth dimension serial, i.e. variables, you may also generate a correlation matrix for the entire fix of variables using the Data Analysis functionality of EXCEL:

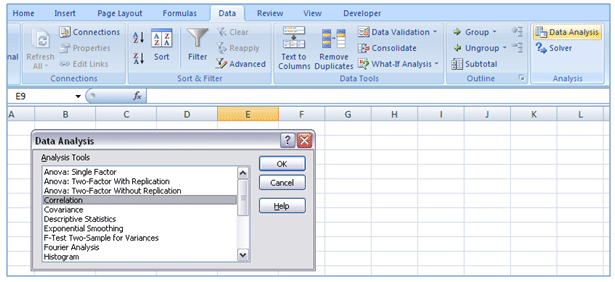
Stride one: Data Tab> Data Assay>Correlation – Click OK

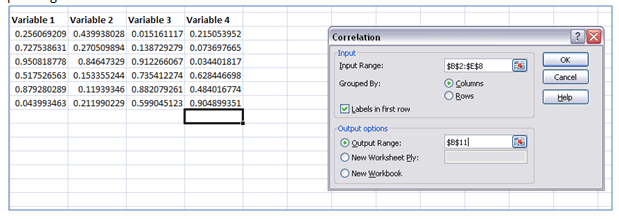
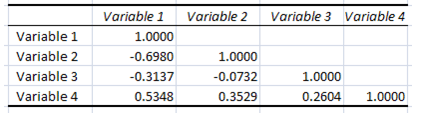
Stride 2: Enter input range, check labels in the first row (if heading selected in input range) and specify output range – Click OK

The resulting correlation matrix is equally follows:

The correlation coefficient, r, can range from -one to +i inclusive. The strength is gauged from the absolute magnitude of r, the greater the accented value of r the stronger will be the relationship between the ii variables. The direction is represented past the sign of the correlation coefficient- a negative sign representing negative correlation; a positive sign indicating a positive correlation. A value of r of -1 or +1 signifies perfectly negative or positive linear correlation respectively. A correlation coefficient of zero indicates that the two variables are not related.

Correlation coefficient assumes that the underlying variables have a linear human relationship with each other. When the underlying relationship is non-linear then the correlation coefficient could lead to faux and misleading results. Correlation could also atomic number 82 to misleading results when there are outliers in the dataset, when data groups are combined inappropriately or when the information is besides homogeneous.

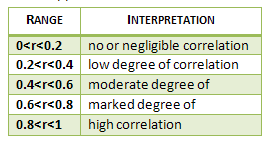
One way of interpreting the strength of the correlation coefficient is by using the post-obit "Rules of Thumb" applied to the absolute value of the calculated measure:

In order to examination whether the correlation is in fact significant rather than a take a chance occurrence we have used hypothesis testing. Specifically, we are testing the mutually exclusive hypotheses:

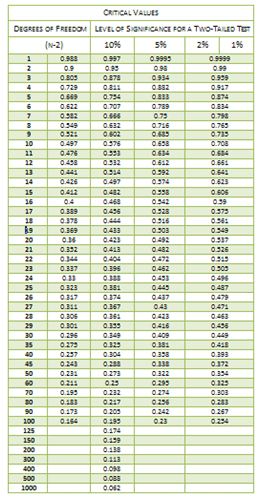
Using a significance level of v%, a two tailed test and due north-2 degrees of freedom (df) (northward is the number of observations), a critical value is determined from the tabular array beneath. If the verbal degrees of freedom is not available in the table and then the critical value at the next lower degrees of freedom will be used. For example, if there are 328 observations, degrees of freedom work out to 326. This value is not present in the tabular array and then we volition use the critical value at the next lower degrees of liberty, i.east. the critical value at degrees of freedom of 300.

If the calculated correlation is greater than the critical value or less than -1×critical value, it can be ended that the calculated correlation is non a adventure finding just is statistically significant. Equally a result, nosotros decline the naught hypothesis and accept the alternative. On the other hand, if the calculated correlation is less than the critical value or greater than -ane×critical value, so nosotros volition conclude that there is no proof of correlation given the dataset and parameters used.

Information technology is important to note that the size of the sample used affects whether a specific observed consequence attains statistical significance. With very large sample sizes, depression correlation values which are demonstrative of a weak relationship between the variables tin can plow out to exist statistically pregnant. This doesn't mean that there is a meaning human relationship between the variables simply just illustrates that the correlation is not zero. Practical significance of the effect should be gauged by the observed force of the relationship, i.e. by its magnitude.

Correlations may change over time. Therefore it is important to summate the correlation coefficient measure for dissimilar analysis periods as well as for unlike window lengths. This is washed to assess the stability of the numerical measure as well equally to place periods when the correlations broke down or changed. For case, an increased value of the correlation coefficient mensurate relative to what usually is expected to event may exist an indication of increased systemic risk in the market.

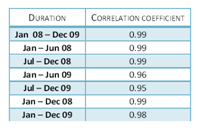
The following table shows the correlation coefficients for WTI and Brent spot prices calculated for various periods. Nosotros tin can see that the measure is relatively stable over fourth dimension.

On the other hand, the table beneath shows the correlation coefficients for WTI and Steel spot prices calculated for periods like to those used above. In this example, we encounter that the measure varies considerably depending on the time frame over which correlations are evaluated.